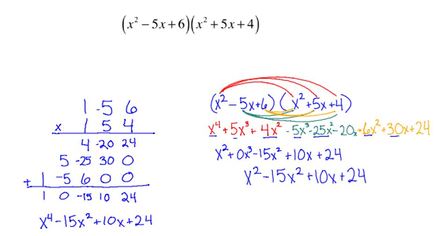Mathematical Processes
Problem SolvingNCTM 1 & ACEI 2d/4Problem solving is a mathematical process through which students acquire and use mathematical knowledge. In my classroom problem solving helps student build mathematical knowledge. Students solve problems that appear in mathematics and other contexts. Problem solving is relevant for all students. I provide students with local and real world problems to solve. My math lessons incorporates problem based learning. A place=based math problem I wrote about similar triangles and trolling poles demonstrates my ability to utilize local real world problems in my classroom. I help students learn to apply a variety of appropriate strategies to solve problems. I also ensure that students monitor and reflect on their problem solving.
|
Reasoning & ProofNCTM 2 & ACEI 2d/4 Reasoning and proof standard is a mathematical process taught at all levels. In my classroom students learn to recognize reasoning and proof as a fundamental part of mathematics. Students do this by making and probing mathematical conjectures. Students develop their own mathematical arguments and proofs. They also evaluate other people’s arguments and proofs. Students reason abstractly and quantitatively. In my early elementary classroom this can take on many forms. One of my favorite ways is for students to act out story problems. In my classroom students are required to construct viable arguments as part of their daily work. They also share their reasoning and proofs which creates the opportunity to critique the reasoning of others.
|
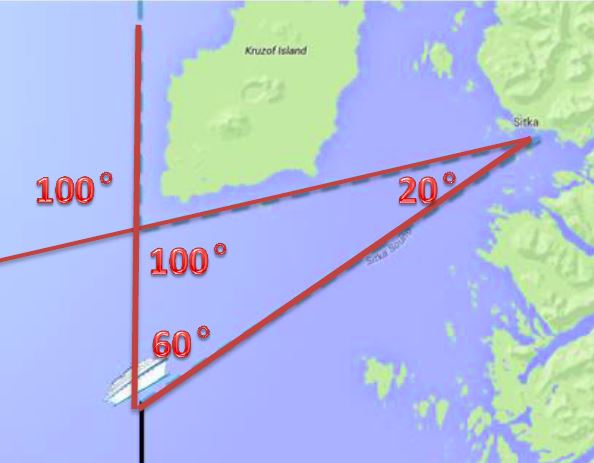
Mathematical CommunicationNCTM 3 & ACEI 2d/4 Teaching students to be able to talk, write, describe and explain math is an important part of developing mathematical thinking. In my classroom. I teach my students to communicate mathematically with precision. I help my students develop the knowledge and skills to use mathematics language to effectively communicate their ideas. Helping students understand math terms and symbols and helping them learn to use them correctly is a foundational skill taught daily. Evidence of this can be found in my community problem about sea turtles in Alaska. I also help my students learn how to use appropriate units of measure and labels. Developing the skills to articulate ideas to others through discussions and exploration helps students develop their mathematical thinking.
|
Mathematical ConnectionNCTM 4 & ACEI 2d/4 In my classroom I connect math with the real world and with other disciplines. I recognize and apply mathematics in context throughout the school day. Integrating math with other discipline areas in real world context is important and will help students understand that math plays a significant role in the world around us. For example I love using the live GPS tracker features of the Iditarod to do real world math.
I also connect mathematical ideas and concepts within mathematics. For example in 2nd grade I teach how arrays and repeated addition are connected to multiplication. I think it is important to recognize and use connections among mathematical concepts and ideas to interconnect and build on one another. |
Mathematical RepresentationNCTM 5 & ACEI 2d/4 Representation in mathematics is the use of symbols, graphs, charts, models, diagrams, and manipulatives as methods of communicating, recording and organizing mathematical ideas and relationships. In my classroom I teach my students to select, apply and translate mathematical representation. I teach my students the importance of using multiple representations. For example, in my class students learn how to represent five groups of four through skip-counting, arrays and through repeated addition. Representation makes make it easier to see and understand and some properties.
|
Mathematical Content
Number and OperationsNCTM Elem & Mid School 9 / ACEI 2d/4Number and operations is about understanding numbers which means learning to represent numbers, relationships among numbers, and number systems. It also means understanding operations and how they relate to one another. Computing fluently is also an important part of number and operations.
In my early elementary classroom understanding number and operations, developing number sense, and gaining arithmetic computation fluency forms the core of my mathematics instruction. Children need to understand the concepts and meanings underlying the operations as opposed to merely applying rules. Many errors in problem solving can be linked back to a lack of or a misunderstanding of place value so I spend a lot of time in my classroom ensuring place value proficiency. I also incorporate estimation and mental math into all my math. The properties of addition and estimation are keys to foundational understanding. The strategy of using concrete, pictorial, abstract in a development, reinforcement, practice way is important as well. |
Different Perspective on AlgebraNCTM Elem & Mid School 10 / ACEI 2d/4Algebra is one my favorite things to teach my students. My students know I love algebra and I love getting them excited about algebra too. I tell my students that doing algebra is like solving a puzzle. I teach them how to be a math detective and to use their math knowledge and skills to solve the problem.
In my classroom algebra involves understanding patterns and relationships. Students represent and analyze mathematical situations using symbols (often shapes). I teach my students to analyze change in simple contexts. Teaching algebraic thinking helps my students build a solid foundation of understanding and mindset for more advanced work in algebra in middle school and high school. |
GeometriesNCTM Elem & Mid School 11 / ACEI 2d/4Geometry is analyzing characteristics and properties of two- and three-dimensional geometric shapes. Students use special relationship to describe locations using coordinate geometry and other representational systems. In my classroom students also learn to apply transformations and use symmetry. Students use visualization, geometric modeling and spatial reason to gain understanding.
|
Data Analysis, Statistics, and ProbabilityNCTM Elem 12 & Mid School 14 / ACEI 2d/4If Algebra is my favorite are of math then data analysis, statistics and probability is a close second. Statistics and probability, while not labeled as a domain in elementary math are introduced. When looking at the concept category of Statistic and Probability in the Alaska Common Core standards you can see that it is built upon the domain Measurement and Data.
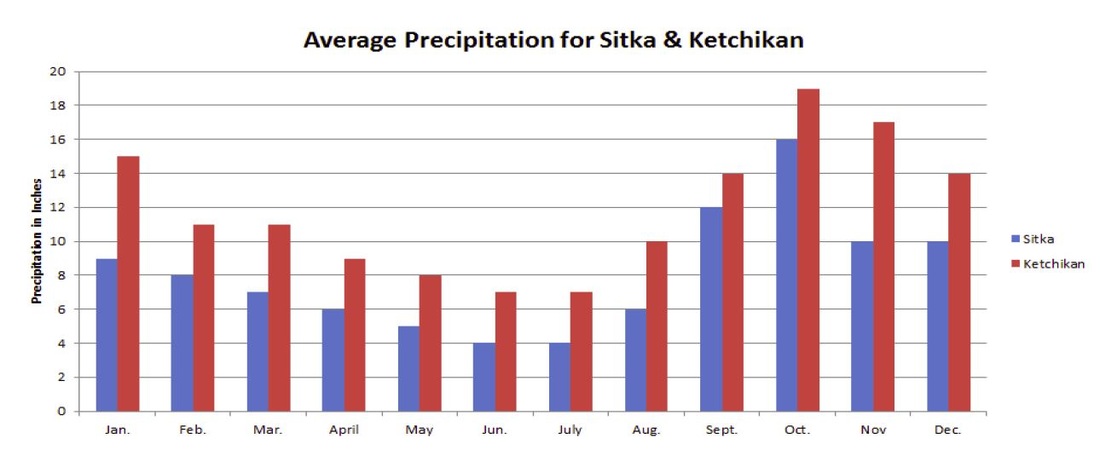
I love to incorporating data analysis, statistics and probability into other areas of the school day. Learning to analyze data is a skill used all the time in real world situations. Everyday my class looks at graphs that are generated from data gathered from their student response systems. In class I demonstrate how students can formulate questions that can be examined with data collection. My students use that data to develop and evaluate inference, predictions and apply basic apply basic concept. |
MeasurementNCTM Elem 13 & Mid School 14 / ACEI 2d/4Measurement is the understanding and skills to measure attributes of objects. Measurement involves learning to apply appropriate methods, tools and formulas to determine measurement. Even though we use measurement everyday (without much thought) it can be very hard for young students to understand at first because measurement is the assignment of a number value to an attribute of an object.
In my early elementary classroom I help my students begin to understand what measureable attributes are. I help them to become familiar with the units and processes for measuring. I help my students understand the measurement of time and money. I also teach my students how to measure the length of an object by selecting and using the appropriate tool. I help students to gain understanding about measurement through estimating and measuring lengths using units of inches, feet, centimeters and meters. |
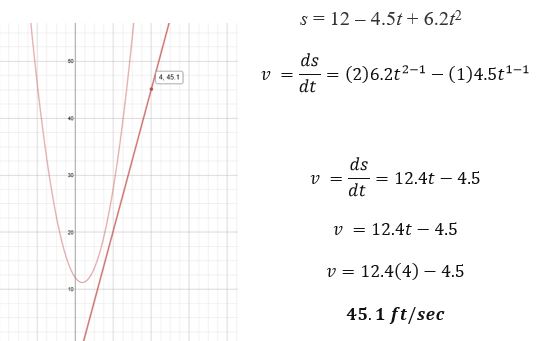
Trigonometry & CalculusNCTM Mid School 12 / ACEI 2d/4As a math teacher it is important to have a conceptual understanding of basic trigonometry and calculus concepts. A teacher may be able to teach arithmetic without understanding algebra, just like a teacher can teach algebra without knowing calculus. However it would be like driving a car without knowing your destination. If you know where you are taking your students you can help them prepare. Calculus is to algebra what algebra is to arithmetic. Knowing how basic principles of mathematics expand to patterns of change between equations can strengthen the teaching of even elementary mathematics.
I don’t expect my students to be able to demonstrate knowledge of limits, continuity, the derivative and problem solving using derivate concepts but I can help students develop solid foundations that will help them as them move into complex studies of change. In my classroom I help my students to understand patterns, equations, geometry, measurement, algebraic thinking, etc. One of the best ways I can prepare my students for calculus is by establishing the right math mindset so students will be motivated and embrace the rigor and challenge of calculus. |
Discrete MathNCTM Mid School 13 / ACEI 2d/4Discrete math is becoming a favorite area of math for me. Understanding just how much computers are dependent on discrete math is fascinating. Computer science is now a basic skill. Every student needs computer science and it should be a part of every classroom which means that our students need discrete math more now than ever.
In my classroom I teach programing and coding. Discrete math is key to programing. My students are learning computational, algorithmic and logical thinking without even realizing it. I use programs like code.org that has great hands on discrete math activities (many of which don’t require a computer or screen). |
Graph Paper Programming - Code.org |
Connections across the Curriculum
NCTM 4 / ACEI #2a,iIn real life content does not appear in isolation but rather it is connected across various areas and disciplines. When you make math relevant across the curriculum you motivate students to learn. You help students to see the purpose and to draw upon their understating of other areas to improve their math skills.
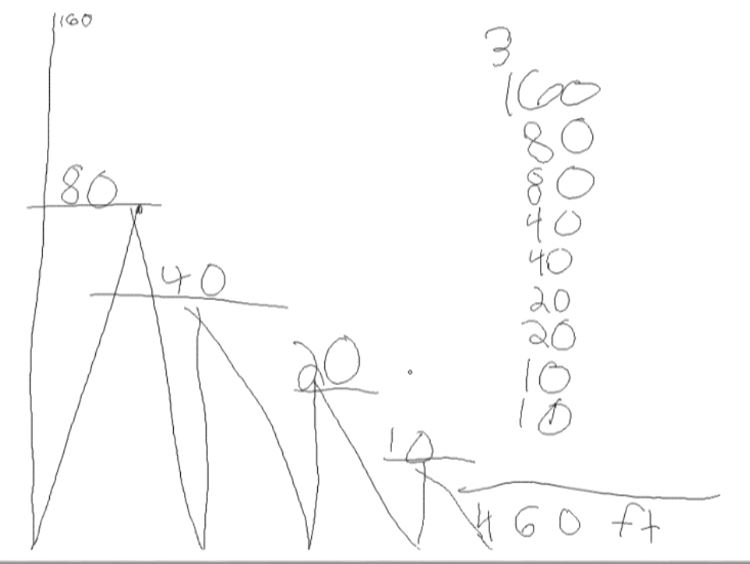
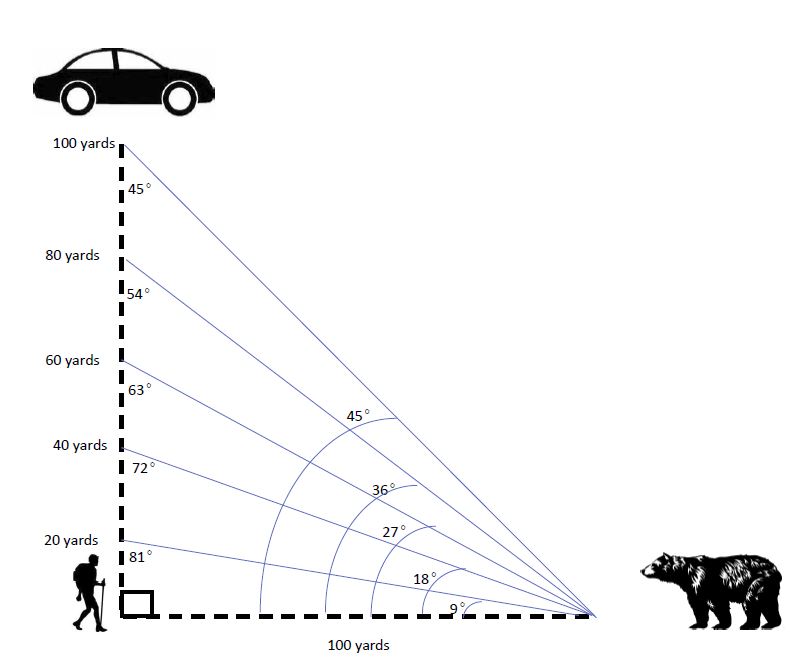
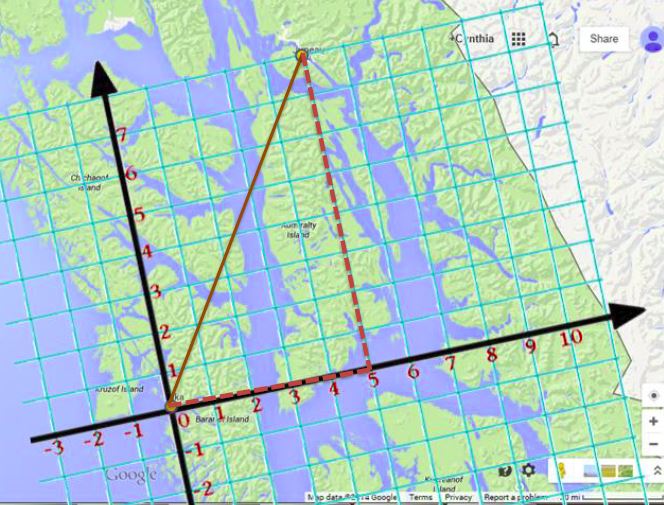
In my classroom I help student experience those connections to enrich authentic learning. For example instead of teaching students about rates in isolation I can introduce rates through dog mushing. By using the Iditarod, geography and live gps tracking I can make the content come alive. In this particular lesson students become interested and motivated to learn and understand the concept of rates to help them make successful prediction about the race. Another example of how I connect content across the curriculum is evident in my distance formula shared community problem. In this problem students use technology, mapping, coordinate plane to find the distance between two locations. Integrating math with things like literature, geography, science, culture, art, and technology brings a new purpose to math. Student learn best when they can make connections with pervious learned knowledge. Whether content is integrate through project-based learning or another practice, my emphasis is always on authentic and rigorous problem-solving. |
Proudly powered by Weebly